Whole numbers are not closed under subtraction. For example, the closure under subtraction of the set of natural numbers, viewed as a subset of the real numbers, is the set of integers.
Which Set Of Numbers Is Closed Under Subtraction. As an opposite example, negative numbers are a closed set under addition. Negative numbers are closed under addition. So, if you try it with negative numbers and subtraction, you can quickly find examples where subtracting negative numbers gives a positive number as a result. For example, the closure under subtraction of the set of natural numbers, viewed as a subset of the real numbers, is the set of integers.
Topic: Prime Numbers From studylib.net
Related Post Topic: Prime Numbers :
A set that is closed under an operation or collection of operations is said to satisfy a closure property. −5 is not a whole number (whole numbers can�t be negative) so: They are not closed under division because, for example, 1 , 0 ∈. No.to say a set is closed under subtraction means that if you subtract any 2 numbers in the set, the answer will always be a member of the set.
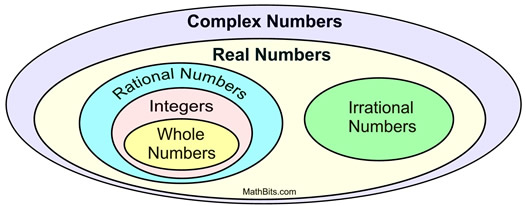
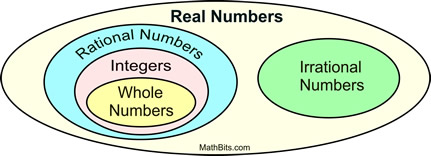
Integers provide closure under subtraction, while whole numbers do not.
Prime numbers are closed under subtraction. They are not closed under division because, for example, 1 , 0 ∈. −5 is not a whole number (whole numbers can�t be negative) so: Natural numbers are closed under division. Which set is closed under subtraction? Thus, we see that for addition, subtraction as well as multiplication, the result that we get is itself a rational number.
Source: chegg.com
Negative integers, integers and rational numbers are the sets of numbers among the choices given in the question that are closed under subtraction. A/b + c/d = (ad+bc)/bd, so closed under addition. Which of the following sets are closed under subtraction?
Source: chegg.com
The set of real numbers is closed under subtraction because a, b ∈ r does imply a − b ∈ r. Irrational numbers $$\mathbb{i}$$ we have seen that any rational number can be expressed as an integer, decimal or exact decimal number. Negative integers, integers and rational numbers are the sets of numbers among the choices given in the question that are closed under subtraction.
Source: studylib.net
The notion of closure is generalized by galois connection , and further by monads. System of whole numbers is not closed under subtraction, this means that the difference of any two whole numbers is not always a whole number. This is a general idea, and.
Source: slideplayer.com
The notion of closure is generalized by galois connection , and further by monads. A/b * c/d = (ac)/(bd), so closed under. 4 − 9 = −5.
Source: slideplayer.com
Which set is closed under subtraction? Thus, we see that for addition, subtraction as well as multiplication, the result that we get is itself a rational number. An important example is that of topological closure.
Source: mathbitsnotebook.com
Two whole numbers the result is also a whole number, but if we try subtracting two such numbers it is possible to get a number that is not in the set. D) the set of natural numbers is not closed under the operation of subtraction because when you subtract one natural number from another, you don’t always get another natural number. The set of real numbers is closed under subtraction because a, b ∈ r does imply a − b ∈ r.
Source: study.com
The notion of closure is generalized by galois connection , and further by monads. This same set is not closed under subtraction since 1 −. They are not closed under division because, for example, 1 , 0 ∈.
Source: meritnation.com
Natural numbers are closed under division. A set is ___ (under an operation) if the operation always produces an element of the same set. This is a general idea, and.
Source: mathbitsnotebook.com
So, if you try it with negative numbers and subtraction, you can quickly find examples where subtracting negative numbers gives a positive number as a result. If an element outside the set is produced, then the operation is not ___. At some point, people were confronted with the problem of having to divide one thing among more than one person.
Source: brainly.in
The natural numbers are closed under addition means that if i add two natural numbers, the sum will also be a natural number. The set of real numbers is closed under subtraction because a, b ∈ r does imply a − b ∈ r. Actually, when you subtract odd numbers, you always get an even number!
Source: youtube.com
An important example is that of topological closure. The set of real numbers is closed under subtraction because a, b ∈ r does imply a − b ∈ r. As an opposite example, negative numbers are a closed set under addition.
Source: slideplayer.com
Subtraction requires 0 and negative integers; Thus, rational numbers are closed under addition, subtraction and multiplication. Click here to see full answer
Source: youtube.com
The set of real numbers is closed under subtraction because a, b ∈ r does imply a − b ∈ r. For example, the closure under subtraction of the set of natural numbers, viewed as a subset of the real numbers, is the set of integers. For example, the closure under subtraction of the set of natural numbers, viewed as a subset of the real numbers, is the set of integers.
Source: brainly.com
At some point, people were confronted with the problem of having to divide one thing among more than one person. Prime numbers are closed under subtraction. The correct options among all the options that are given in the question are options b, c and d.
Source: youtube.com
For example, the closure under subtraction of the set of natural numbers, viewed as a subset of the real numbers, is the set of integers. Two whole numbers the result is also a whole number, but if we try subtracting two such numbers it is possible to get a number that is not in the set. A set that is closed under an operation or collection of operations is said to satisfy a closure property.
Source: slideplayer.com
Natural numbers are closed under division. Usually (not generally) it involves an operation, for example: So, the set of negative numbers is not closed to subtraction.
Source: youtube.com
The natural numbers are closed under addition means that if i add two natural numbers, the sum will also be a natural number. No, subtraction is not closed on the set of natural numbers. At some point, people were confronted with the problem of having to divide one thing among more than one person.
Source: slidetodoc.com
Natural numbers are closed under division. Click here to see full answer The set of real numbers is closed under subtraction because a, b ∈ r does imply a − b ∈ r.
Source: chegg.com
As an opposite example, negative numbers are a closed set under addition. Negative numbers are closed under addition. If you subtract two whole numbers, you do not always get a whole number.
Source: brainly.in
Which set is closed under subtraction? As an opposite example, negative numbers are a closed set under addition. D) the set of natural numbers is not closed under the operation of subtraction because when you subtract one natural number from another, you don’t always get another natural number.
Also Read :
