For any two rational numbers, say x and y, the results of addition, subtraction and multiplication operations give a rational number. Add, subtract, and multiply polynomials.
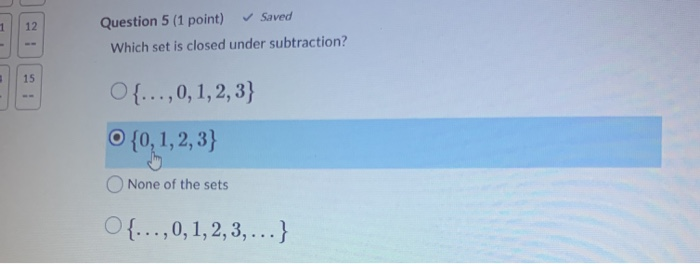
Which Set Is Closed Under Subtraction. It�s a nice way of getting organized and. So the set of whole numbers is not closed under subtraction. The difference between any two rational numbers will always be a rational number, i.e. Whole numbers are not closed under subtraction.
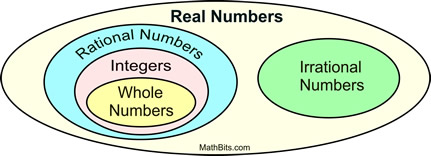Number Systems- Mathbitsnotebook (Jr) From mathbitsnotebook.com
Related Post Number Systems- Mathbitsnotebook (Jr) :
Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; As you see, a closed set ($y$ in this definition) is a subset of another set ($x$ in this definition), and the operation may take and give members of $x$ which are not in $y$. A set is closed under an operation if the results of that operation always lies in that set. Is the set {0, 1} closed under division?
Now we can say that the set of whole numbers is closed under addition.
Use closure tables to answer each of the following questions. Whole numbers are not closed under subtraction. A set is closed under subtraction means if you can subtract any two numbers in the set and still have a number in the set as a result. We can say that rational numbers are closed under addition, subtraction and multiplication. The set of real numbers is closed under subtraction because a, b ∈ r does imply a − b ∈ r. Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication;
Source: brainly.com
For any two rational numbers, say x and y, the results of addition, subtraction and multiplication operations give a rational number. Plication, but the set of whole numbers is not closed under subtraction. Therefore, the set of integers under subtraction is not a group!
Source: mathsmd.com
For two rational numbers say x and y the results of addition, subtraction and multiplication operations give a rational number. Let us say ‘a’ and ‘b’ are two integers either positive or negative, their result should always be an integer, i.e (a + b) would always be an integer. For instance, the set {1,−1} is closed under multiplication but not subtraction.
Source: study.com
Note that closure under an operation depends on both the operation and the set. (notice also that this set is closed, but does not have an identity and therefore also does not have the inverse property.) 4) the set of natural numbers under addition is not a group , because it does not satisfy all of the group properties: The set of integers is closed under addition.
Source: youtube.com
Explanation integers are closed under subtraction which mean that subtraction of integers will also give integers. Add, subtract, and multiply polynomials. For any two rational numbers, say x and y, the results of addition, subtraction and multiplication operations give a rational number.
Source: chegg.com
The answer is no, we can�t get out of the set of integers by subtracting, so the set of integers is closed under subtraction. The set of integers is closed under subtraction. Before understanding this topic you must know what are whole numbers ?
Source: slideplayer.com
Add, subtract, and multiply polynomials. Now we can say that the set of whole numbers is closed under addition. Set {0, 1} so this set is closed under multiplication.
![Solved] 1.Is The Set Of Rational Expressions Closed Under Subtraction?Explain P(X)/Q(X) - R(X)/S(X) = 2.Is The Set Of Rational Expressions Closed Un… | Course Hero](https://www.coursehero.com/qa/attachment/14590262/ “Solved] 1.Is The Set Of Rational Expressions Closed Under Subtraction?Explain P(X)/Q(X) - R(X)/S(X) = 2.Is The Set Of Rational Expressions Closed Un… | Course Hero”) Source: coursehero.com
4 − 9 = −5. (notice also that this set is closed, but does not have an identity and therefore also does not have the inverse property.) 4) the set of natural numbers under addition is not a group , because it does not satisfy all of the group properties: Set {0, 1} so this set is closed under multiplication.
Source: chegg.com
The difference between any two rational numbers will always be a rational number, i.e. The set of integers is closed under multiplication. Thus z, which contains sets, is not closed under subtraction.
Source: slideserve.com
For two rational numbers say x and y the results of addition, subtraction and multiplication operations give a rational number. Is the set {0, 1} closed under subtraction? Is the set {0, 1} closed under addition?
Source: youtube.com
Do you know why division is not under closure. But the set of integers is not closed under division. A ring is a nonempty set r with two binary operations (usually written as addition and multiplication) such that for all a;b;c 2 r, (1) r is closed under addition:
Source: chegg.com
A set is closed under subtraction means if you can subtract any two numbers in the set and still have a number in the set as a result. This closure game is fun. Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication;
Source: mathbitsnotebook.com
The set of integers is closed under subtraction. This smallest closed set is called the closure of s (with respect to these operations). Before understanding this topic you must know what are whole numbers ?
Source: qa-all.com
The sum we get is 11 which as we know is a whole number. It�s a nice way of getting organized and. D) the set of natural numbers is not closed under the operation of subtraction because when you subtract one natural number from another, you don’t always get another natural number.
Source: learnzillion.com
The set of integers is closed under multiplication. Terms in this set (26) closure property a set is closed under an operation if the operation on two elements of the set always produces another element of the set. A ring is a nonempty set r with two binary operations (usually written as addition and multiplication) such that for all a;b;c 2 r, (1) r is closed under addition:
Source: slideplayer.com
The set that is not closed under subtraction is b) z. This closure game is fun. It does not have the identity property (see the.
Source: brainly.in
But the set of integers is not closed under division. Is the set {0, 1} closed under subtraction? Closure property of rational numbers under multiplication:
Source: slideplayer.com
A set is closed under subtraction means if you can subtract any two numbers in the set and still have a number in the set as a result. It�s a nice way of getting organized and. Therefore, the set of integers under subtraction is not a group!
Source: meritnation.com
This smallest closed set is called the closure of s (with respect to these operations). Thus z, which contains sets, is not closed under subtraction. For example, the closure under subtraction of the set of natural numbers, viewed as a subset of the real numbers, is the set of integers.
Source: brainly.com
Because of this, it follows that real numbers are also closed under subtraction and division (except division by 0). A set is closed under an operation if the results of that operation always lies in that set. Closure property of rational numbers under subtraction:
Source: brainly.in
A ring is a nonempty set r with two binary operations (usually written as addition and multiplication) such that for all a;b;c 2 r, (1) r is closed under addition: Is the set {0, 1} closed under division? (notice also that this set is closed, but does not have an identity and therefore also does not have the inverse property.) 4) the set of natural numbers under addition is not a group , because it does not satisfy all of the group properties:
Also Read :
