Everything below and to the left of the line is shaded. Which ordered pairs make both inequalities true?
Which Ordered Pair Makes Both Inequalities True. Everything to the left of the line is shaded. If a ordered pair make both inequalities true, then the ordered pair is a solution of the system of inequalities. Everything to the right of the line is shaded. Which ordered pair makes both inequalities true?
Which Ordered Pair Makes Both Inequalities True? Y < -X + 1 And Y > X? (-3, 5), (-2, 2), (-1, -3), (0, -1) From cuemath.com
Related Post Which Ordered Pair Makes Both Inequalities True? Y < -X + 1 And Y > X? (-3, 5), (-2, 2), (-1, -3), (0, -1) :
These have the same first coordinate and different second coordinates. Everything to the left of the line is shaded. Which ordered pairs make both inequalities true? Which ordered pair makes both inequalities true?
The ordered pair (4,0) makes both inequalities true.
Which ordered pairs make both inequalities true? Which system of linear inequalities is represented by the graph? The first solid line has a negative slope and goes through (0, 1) and (1, 0). The ordered pair (4,0) makes both inequalities true. The first solid line has a positive slope and goes through (0, negative 2) and (1, 0). When a and b are both positive or both negative:
Source: gauthmath.com
Each hardcover book cost $1.50, and each paperback book cost $0.50. Which ordered pair makes both inequalities true? Which system of linear inequalities is represented by the graph?
Source: cuemath.com
Everything to the right of the line is. You are given two inequalities: Everything below and to the left of the line is shaded.
Source: gauthmath.com
The second dashed line has a negative slope and goes through (0, 3) and (1, 1). Tap card to see definition 👆. Due to the last inequality, you can eliminate the last two ordered pair.
Source: brainly.com
Each hardcover book cost $1.50, and each paperback book cost $0.50. Ok so basically you need to cut the shape in half so it makes two squares. Gillian purchased 25 books at the library book sale.
Source: brainly.com
The second dashed line has a negative slope and goes through (0, 3) and (1, 0). Which system of linear inequalities is represented by the graph? These have the same first coordinate and different second coordinates.
Source: brainly.com
The ordered pair which makes both inequalities true are ( 3, 0 ). If a ordered pair make both inequalities true, then the ordered pair is a solution of the system of inequalities. These have the same first coordinate and different second coordinates.
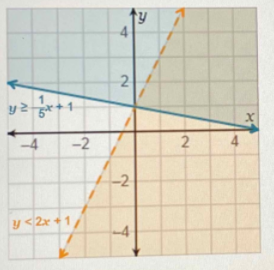Source: snapsolve.com
The first solid line has a negative slope and goes through (0, 1) and (1, 0). If a ordered pair is a solution of the system of inequalities, then the ordered pair lie in the shaded area of the solution set of the system. The second example is not a function, because it contains the ordered pairs (1,2) and (1,5).
Source: brainly.com
All you gotta do from there is times l x w of both squared and add both together if that makes sense. Which is true about the solution to the system of inequalities shown? The second dashed line has a negative slope and goes through (0, 3) and (1, 1).
Source: gauthmath.com
Everything to the right of the line is. The first solid line has a positive slope and goes through (0, negative 2) and (1, 0). The first solid line has a positive slope and goes through (0, negative 2) and (1, 0).
Source: brainly.com
Due to the last inequality, you can eliminate the last two ordered pair. This is the best answer 👇. Everything to the right of the line is shaded.
![Solved] Which Ordered Pairs Make Both Inequalities True? Check All That Apply. (–2, 2) (0, - Brainly.com](https://us-static.z-dn.net/files/dd6/517dfadebdeca618d8641ca9596a8b55.png “Solved] Which Ordered Pairs Make Both Inequalities True? Check All That Apply. (–2, 2) (0, - Brainly.com”) Source: brainly.com
The second dashed line has a positive slope and goes through (negative 1, negative 1) and (1, 1). Everything to the right of the line is. The ordered pair (4,0) makes both inequalities true.
Source: brainly.com
Which ordered pair makes both inequalities true? Has a line by 2 and 3. If a ordered pair make both inequalities true, then the ordered pair is a solution of the system of inequalities.
Source: brainly.com
Which ordered pair makes both inequalities true? The ordered pair (4,0) lie in the shaded area of the solution set. Tap card to see definition 👆.
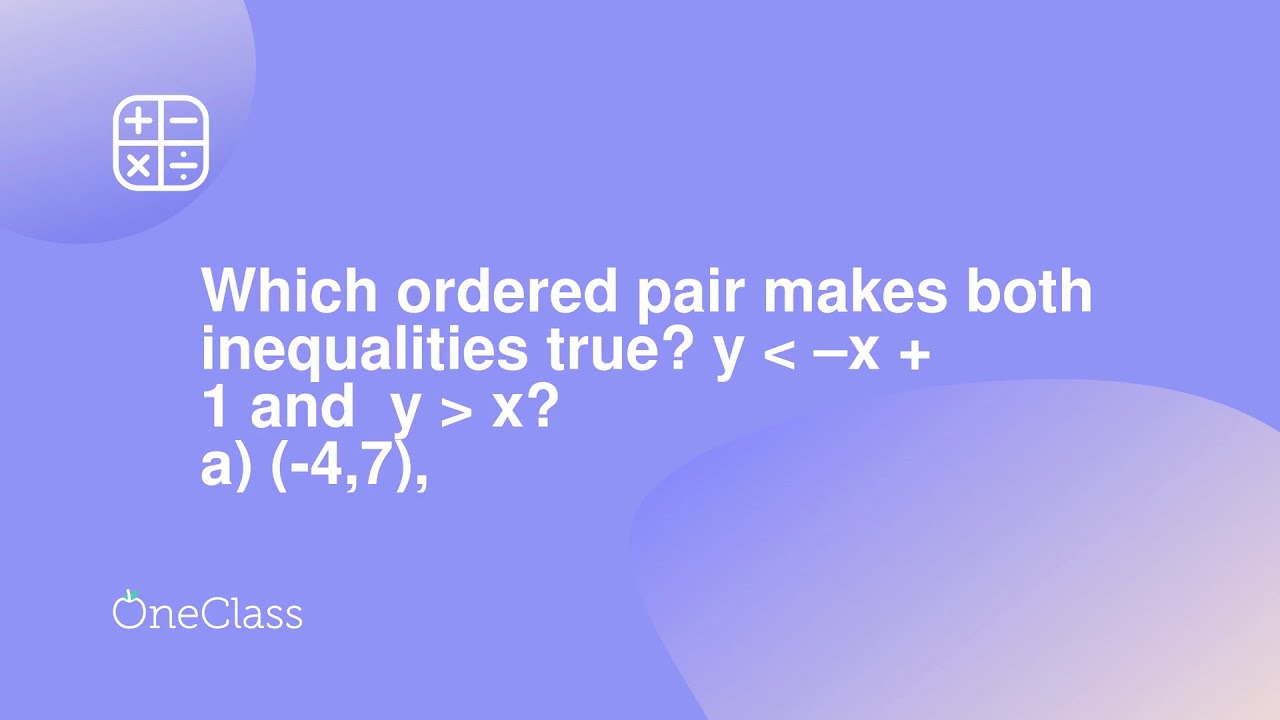Source: youtube.com
If a ordered pair make both inequalities true, then the ordered pair is a solution of the system of inequalities. If a ordered pair is a solution of the system of inequalities, then the ordered pair lie in the shaded area of the solution set of the system. If an ordered pair makes both inequalities true, then the ordered pair must lie in the shaded area of the inequalities system solution set.
Source: brainly.com
The second example is not a function, because it contains the ordered pairs (1,2) and (1,5). Which ordered pairs make both inequalities true? Everything below and to the left of the line is shaded.
Source: brainly.com
The second dashed line has a negative slope and goes through (0, 3) and (1, 0). Gillian purchased 25 books at the library book sale. Which ordered pair makes both inequalities true?
Source: brainly.com
Due to the last inequality, you can eliminate the last two ordered pair. The first solid line has a positive slope and goes through (0, negative 2) and (2, 0). The first solid line has a positive slope and goes through (0, negative 2) and (1, 0).
Source: chegg.com
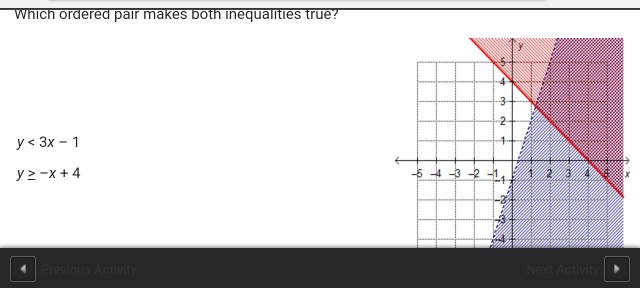
Which ordered pair makes both inequalities true? Which ordered pairs make both inequalities true? This is the best answer 👇.
Source: gauthmath.com
Which ordered pair makes both inequalities true? The second dashed line has a negative slope and goes through (0, 3) and (1, 0). The first solid line has a negative slope and goes through (0, 1) and (1, 0).
Source: brainly.com
Which ordered pairs make both inequalities true? Due to the last inequality, you can eliminate the last two ordered pair. Which system of linear inequalities is represented by the graph?
Also Read :
