That’s true in certain cases.(namely, multiplying some quantity x by a n. They are closed under subtraction.
Which Of The Following Sets Is Closed Under Subtraction. 2 see answers mansiverma82 mansiverma82 answer: So we�re giving that a set of numbers is considered close under an operation. Two whole numbers the result is also a whole number, but if we try subtracting two such numbers it is possible to get a number that is not in the set. Whole numbers are not closed under subtraction.
Solved Are The Following Sets Closed Under The Given | Chegg.com From chegg.com
Related Post Solved Are The Following Sets Closed Under The Given | Chegg.com :
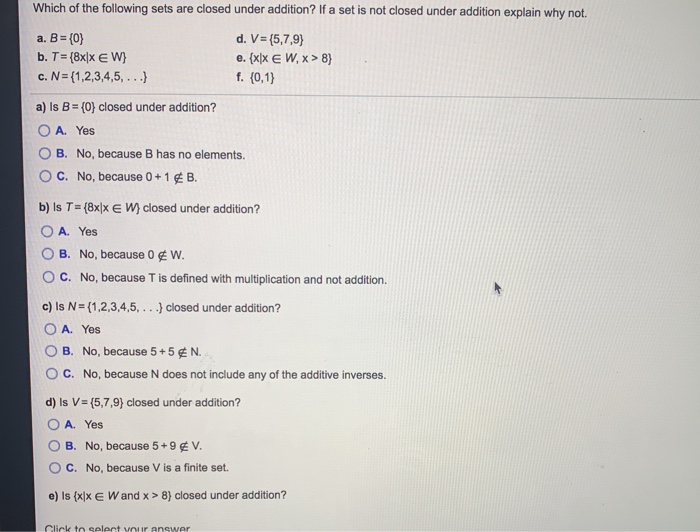
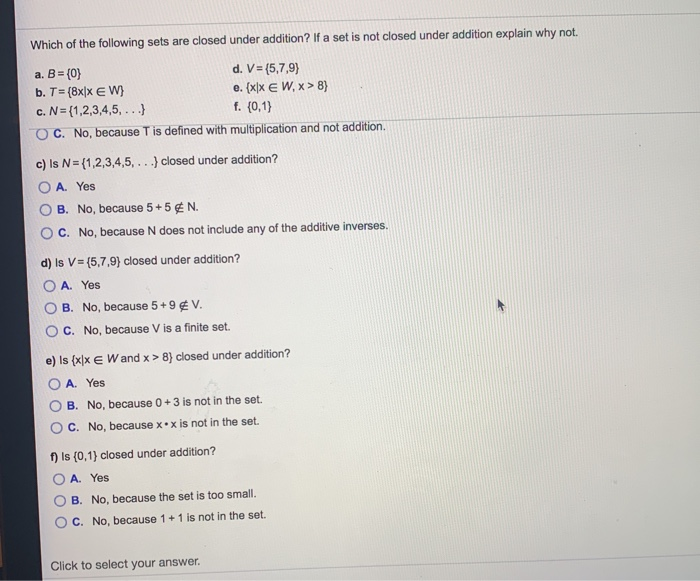
Addition division multiplication subtraction none determine whether the set. Is the set {0, 1} closed under subtraction? Rational numbers are closed under addition, subtraction, multiplication, as well as division by a nonzero rational. A set, well defined collection of objects such as numbers, is considered closed under a specific operation if applying that operation to two members of the set will result in.
So, closed under subtraction means if we subtract two numbers of a set than it must belong to that set.
They are not closed under subtraction. Is the set {0, 1} closed under division? From this dilemma came the set of rational numbers. Subtracting two whole numbers might not make a whole number. So here we have our positive vintages and subjection. Integers provide closure under subtraction, while whole numbers do not.
Source: youtube.com
The set of rational numbers. For example, the positive integers are closed under addition, but not under subtraction: Whole numbers are (1,2,3,4,5.) now,take any 2 numbers and add them.
Source: brainly.com
Log in for more information. So this is a negative and stir so we see that this set is an operation is not closed. Note that closure under an operation depends on both the operation and the set.
Source: slideplayer.com
The set of irrational numbers. A set that is closed under an operation or collection of operations is said to satisfy a closure property. For example, the positive integers are closed under addition, but not under subtraction:
Source: chegg.com
A set is closed under addition if you can add any two numbers in the set and still have a number in the set as a result. Since, if we subtract two integers it will be an integer only. I generally see closed under some.
Source: numerade.com
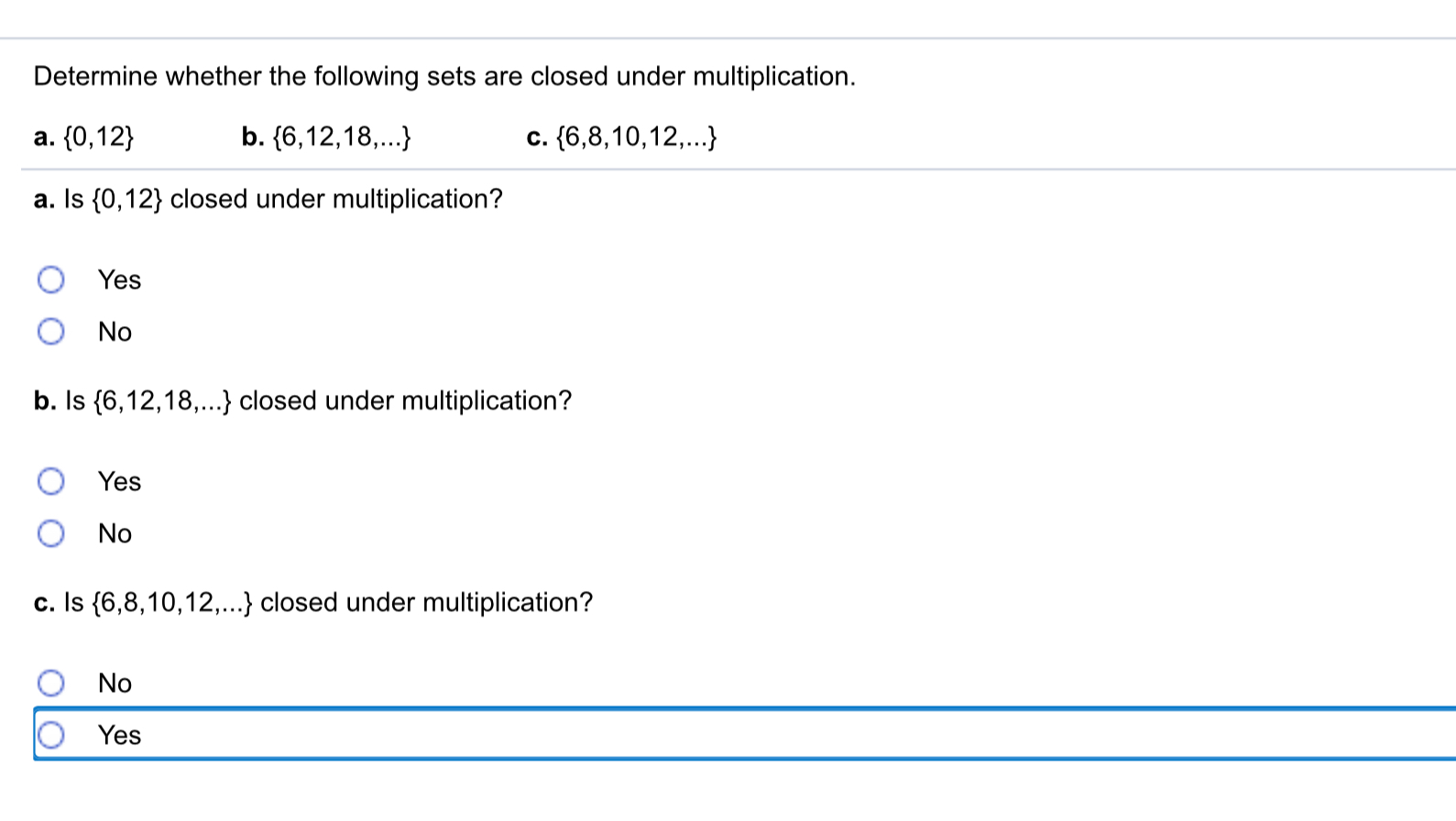
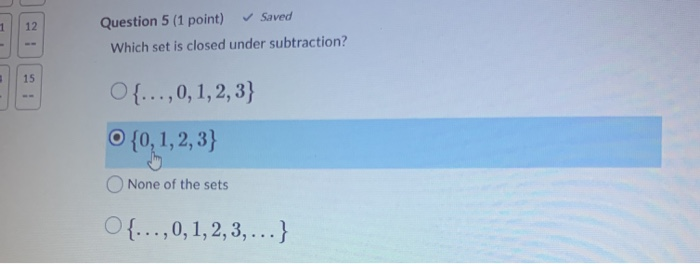
A set, well defined collection of objects such as numbers, is considered closed under a specific operation if applying that operation to two members of the set will result in. Two whole numbers the result is also a whole number, but if we try subtracting two such numbers it is possible to get a number that is not in the set. Which of the following sets are closed under subtraction?
Source: bartleby.com
A set of elements is closed under an operation if, when you apply the operation to elements of the set, you always get another element of the set. Thus the sets ℂ (complex numbers), ℝ (real numbers), ℚ. So let�s take two positive interviews.
Source: chegg.com
Integers provide closure under subtraction, while whole numbers do not. No.a set is closed under subtraction if when you subtract any two numbers in the set, the answer is always a member of the set.the natural numbers are. 4) every element of the set has an inverse under the operation that is also an element of the set.
Source: brainly.com
Example 2 = explain closure property under subtraction with the help of given integers 7 and 20. Integers are closed under subtraction. A set, well defined collection of objects such as numbers, is considered closed under a specific operation if applying that operation to two members of the set will result in.
Source: chegg.com
They are closed under subtraction. Which of the following sets is not closed under subtraction? So let�s take two positive interviews.
Source: chegg.com
Which of the following sets is not closed under subtraction? That’s true in certain cases.(namely, multiplying some quantity x by a n. Subtracting two whole numbers might not make a whole number.
Source: meritnation.com
But we got to minus three, which is equal to negative one. We cannot answer without seeing the sets. The set is closed under the following.
Source: chegg.com
The set of rational numbers. The sum we get is 11 which as we know is a whole number. I generally see closed under some.
Source: learnzillion.com
Integers are closed under subtraction. Integers are closed under subtraction. Since, if we subtract two integers it will be an integer only.
Source: youtube.com
Which of the following sets is not closed under subtraction? −5 is not a whole number (whole numbers can�t be negative) so: But we got to minus three, which is equal to negative one.
Source: chegg.com
The sum we get is 11 which as we know is a whole number. Closure property of rational numbers under subtraction: 1 − 2 is not a positive integer even though both 1 and 2 are positive integers.
Source: chegg.com
Now, if we subtract these two, if we take a minus b, there should be a positive integer if it�s closed. 1 see answer aryan561451 is waiting for your help. Add your answer and earn points.
Source: study.com
The set of whole numbers. So, closed under subtraction means if we subtract two numbers of a set than it must belong to that set. They are closed under subtraction.
Source: chegg.com
If we enlarge our set to be the integers Whole numbers are (1,2,3,4,5.) now,take any 2 numbers and add them. Integers provide closure under subtraction, while whole numbers do not.
Source: brainly.in
The difference between any two rational numbers will always be a rational number, i.e. Which set is closed under subtraction? Integers are closed under subtraction.
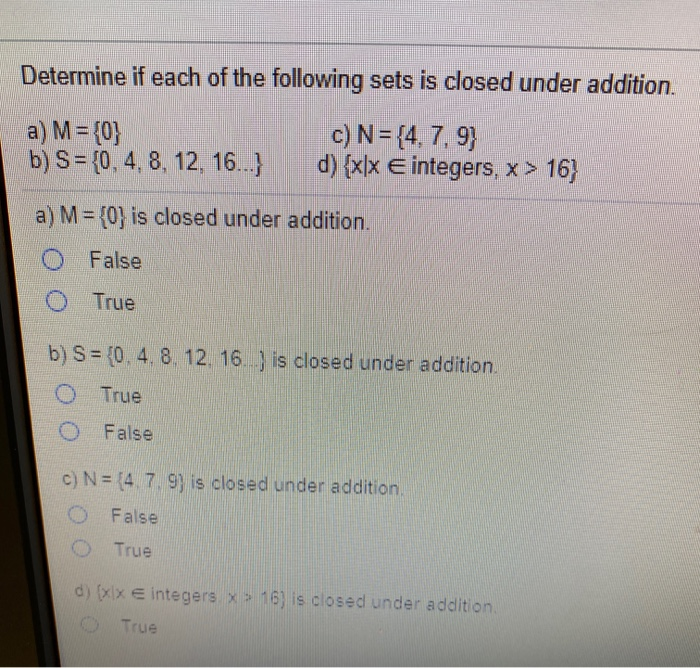Source: chegg.com
“an operation o on a set s is closed if for every pair of elements in the set a and b the result of the operation is also an element of the set.”. Which of the following sets is not closed under subtraction? The difference between any two rational numbers will always be a rational number, i.e.
Also Read :
