If the usage of a comparison test is improper, determine if the series does converge or diverge and provide a correct usage of a comparison test. ¥ page 5 of 10
Which Of The Following Series Converge. If the usage of a comparison test is improper, determine if the series does converge or diverge and provide a correct usage of a comparison test. How many terms are in the series so that the sum of the series first exceeds 100? En=1 vn2+3 +1 a) i only. 10.the radius of convergence for the series ¥ å n=0 n2xn 10n is a.1 b.1/10 c.
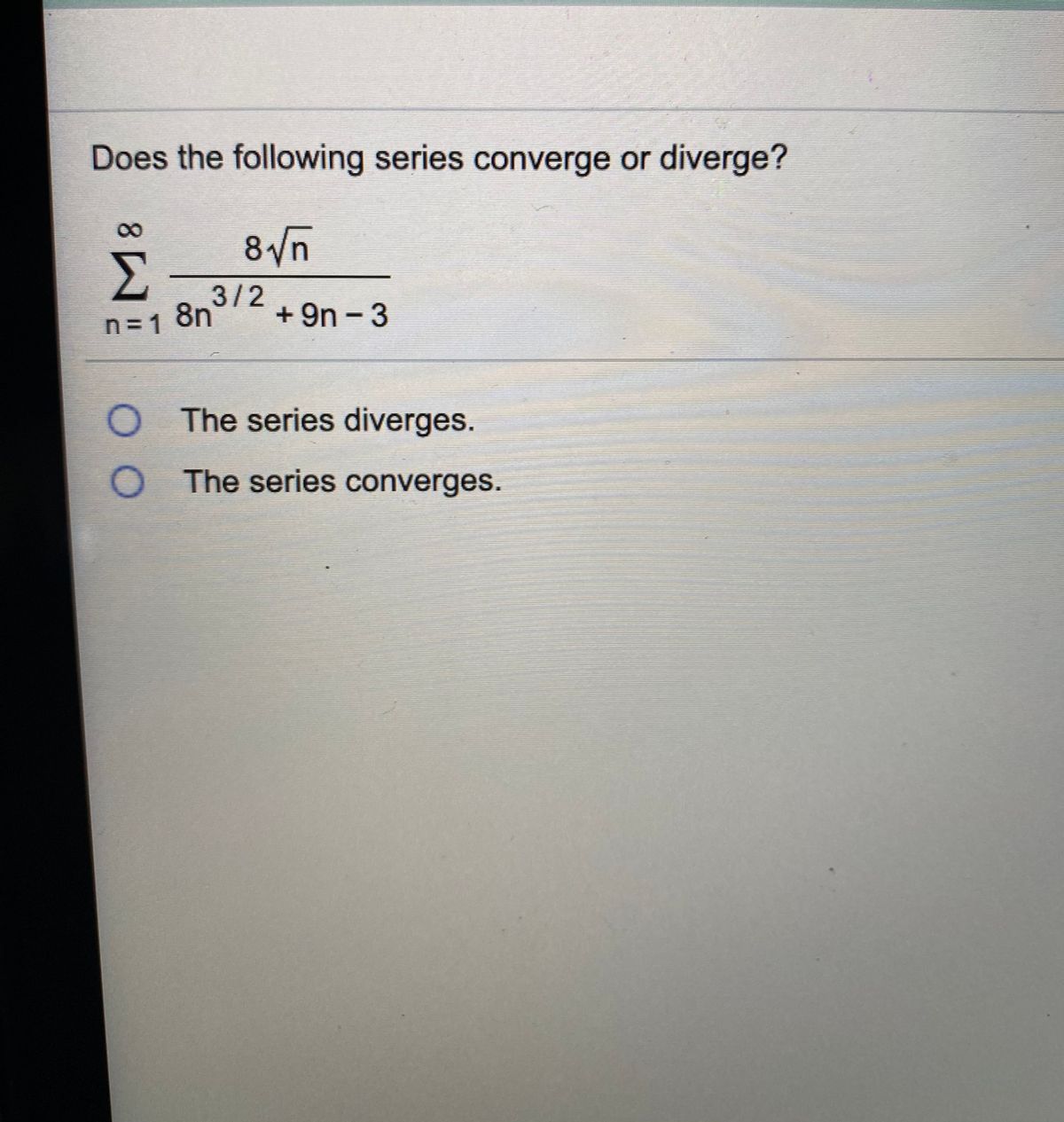Answered: Does The Following Series Converge Or… | Bartleby From bartleby.com
Related Post Answered: Does The Following Series Converge Or… | Bartleby :
Show transcribed image text expert answer. When the above fraction is equal to 1, we cannot us. For the convergent series, if possible, find their exact value; 10.the radius of convergence for the series ¥ å n=0 n2xn 10n is a.1 b.1/10 c.
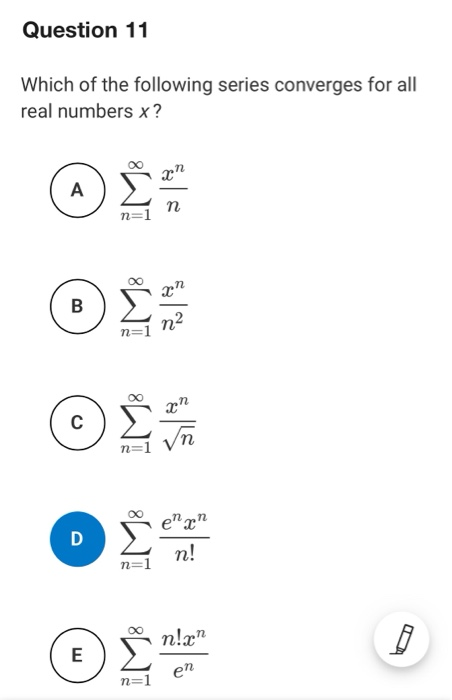
Which of the following series converge?
Let us examine the series for x = ± 1. We review their content and use your feedback to. Experts are tested by chegg as specialists in their subject area. For x = 1, the series reduces to. E.the test cannot be applied to an = 3 4 n+6n 4 and bn = 3 4. How many terms are in the series so that the sum of the series first exceeds 100?
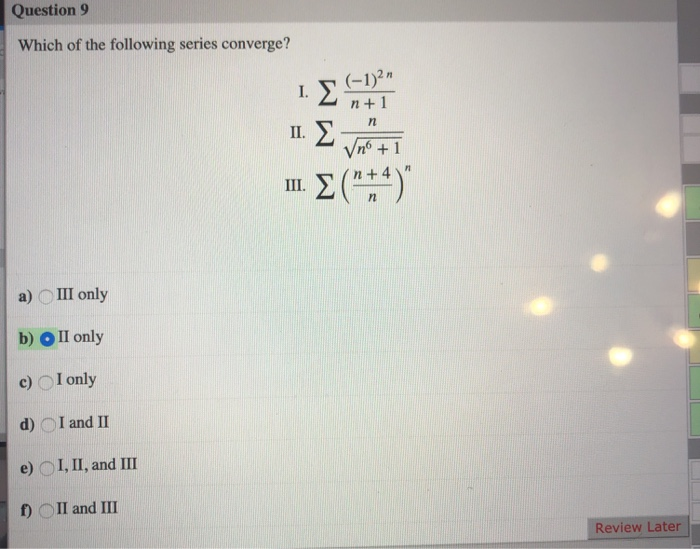Source: chegg.com
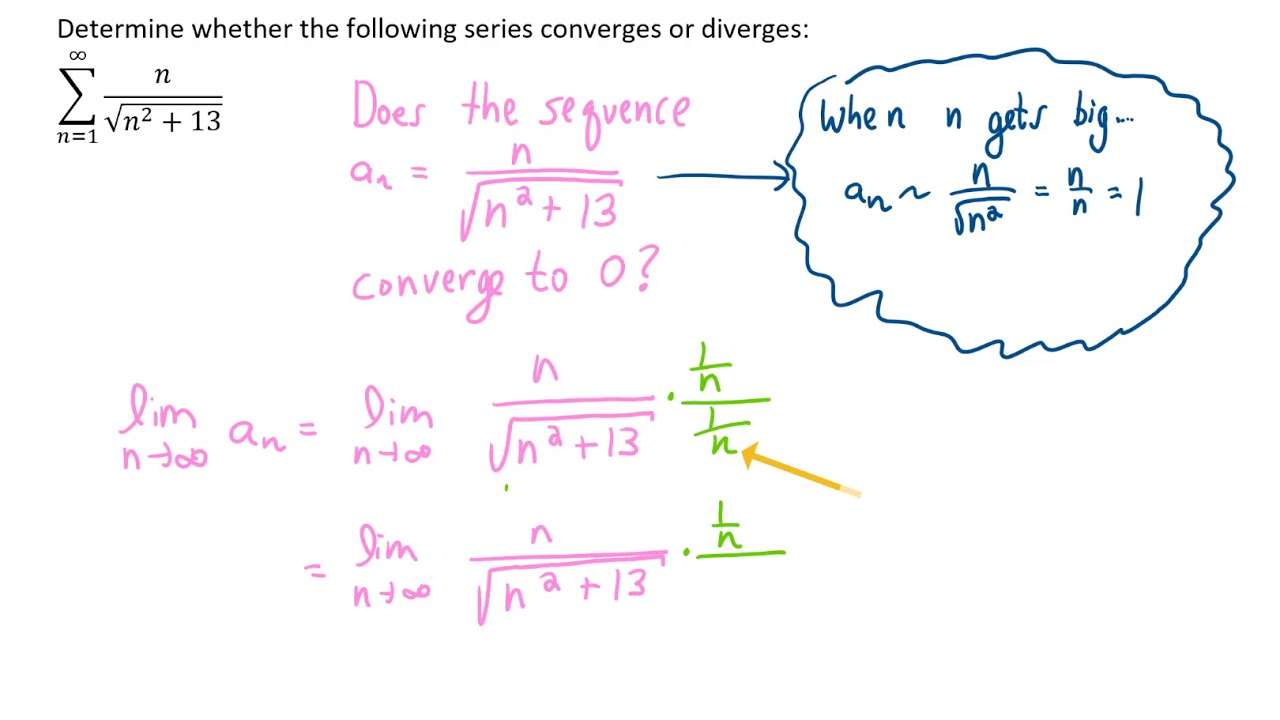
One may recall that each series that converges has its general term tending to 0, here. One may recall that each series that converges has its general term tending to 0, here. The nth term for divergence states that if lim n → ∞ a n does not exist, or if lim n → ∞ (a n ≠ 0), then the series ∑ n = 1 ∞ (a n) is divergent.
Source: bartleby.com
Get the answer to your homework problem. The series ∞ i=1 a i is said to converge absolutely if the series of the absolute values of the terms ∞ i=1 |a i|=|a 1|+|a 2|+··· converges. The limit of the sequence terms is, lim n → ∞ n ( n + 1) 2 = ∞ lim n → ∞ n ( n + 1) 2 = ∞.
Source:
E.the test cannot be applied to an = 3 4 n+6n 4 and bn = 3 4. Match the following series with the series below in which you can compare using the limit comparison test. One may recall that each series that converges has its general term tending to 0, here.
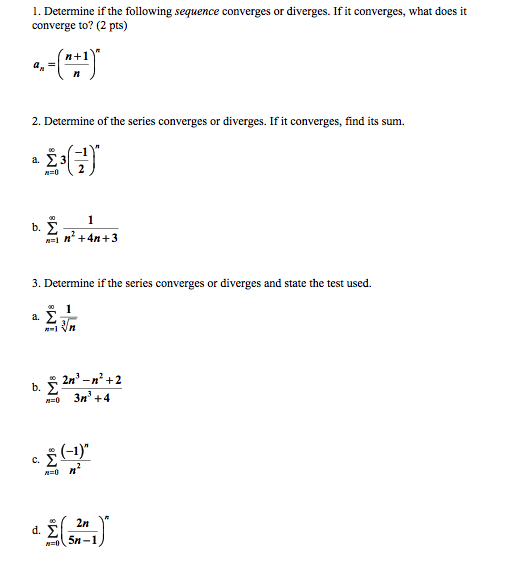Source: oneclass.com
Basically, the substitution makes this exactly the same as considering ∑ 1 n p by the integral test.) 15.4 determine which of the following series converge: En=1 vn2+3 +1 a) i only. When the above fraction is equal to 1, we cannot us.
Source: chegg.com
(a) ∑ ∞ n =2 1 √ n log(n). Otherwise, give the sum of the first five terms, a bound on the approximation error, and the number of terms required find their value to five decimal places. (a) ∑ ∞ n =2 1 √ n log(n).
Source: slideplayer.com
Nth term test for divergence definition. The limit of the sequence terms is, lim n → ∞ n ( n + 1) 2 = ∞ lim n → ∞ n ( n + 1) 2 = ∞. We have learned that if a series converges, then the summed sequence�s terms must converge to 0.
Source: seriestestmjs.weebly.com
Lim n → ∞ ( 1.5) n =? Ln=13 which of the following series converge? Which of the following series converge conditionally?
Source: numerade.com
Get the answer to your homework problem. \sum_ {n=1}^ {\infty }\frac {1} {7^ {n}} c. So, to determine if the series is convergent we will first need to see if the sequence of partial sums, { n ( n + 1) 2 } ∞ n = 1 { n ( n + 1) 2 } n = 1 ∞.
Source: homeworklib.com
Nth term test for divergence definition. See the answer see the answer done loading. The summation from n equals 1 to infinity of 1 over n raised to the negative one half power d.
![Solved]: Which Of The Following Series Converge? 2 _2 2 =](https://media.cheggcdn.com/study/90d/90dbc305-ff66-4829-915d-d75526e114a0/image “Solved]: Which Of The Following Series Converge? 2 _2 2 =") Source: answerparks.com
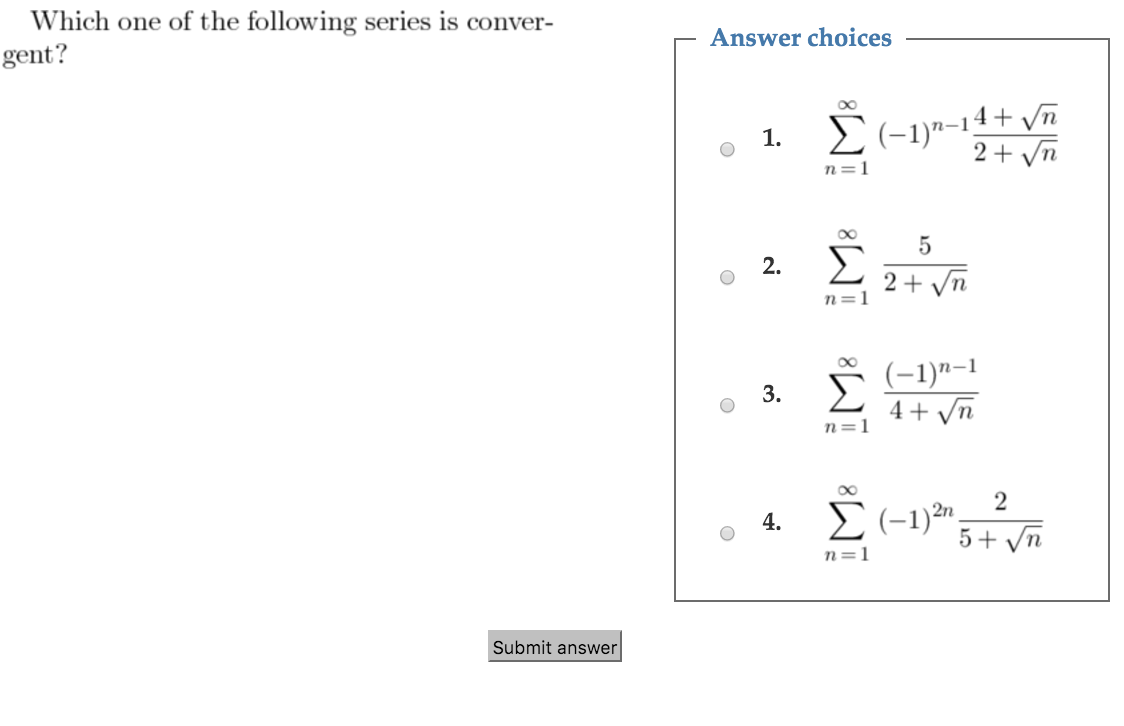
So, for p > 0, by the alternating series test, the series will converge. Converges absolutely n� +1 2/3. Does the series diverge, converge conditionally, or converge absolutely?
Source: youtube.com
\sum_ {n=1}^ {\infty }n^ {4} b. This will converge to 0 when n^p increases monotonically to infinity, which will happen exactly when p > 0. When the above fraction is equal to 1, we cannot us.
Source: chegg.com
En=1 =2 in n =1 n²+3 r+1 a) i only. By ratio test, the given series converges for |x| < 1 and diverges for |x| > 1. The absolute value is bounded above by 1/n!, which has a ratio which converges to 0 (in fact, its sum is e).
Source: chegg.com
Try numerade free for 7 days. For example, the series {9, 5, 1, 0, 0, 0} has settled, or converged, on the number 0. Otherwise, give the sum of the first five terms, a bound on the approximation error, and the number of terms required find their value to five decimal places.
Source: chegg.com
Which of the following series converge conditionally? We have learned that if a series converges, then the summed sequence�s terms must converge to 0. The summation from n equals 1 to infinity of 1 over n raised the the one fourth power c.
Source: itprospt.com
Which of the following series converge? Which of the following are improper uses of the comparison test? The summation from n equals 1 to infinity of 1 over n raised the the one fourth power c.
Source: chegg.com
Show transcribed image text expert answer. If a series converges absolutely then it converges. ¥ page 5 of 10
Source: chegg.com
The nth term for divergence states that if lim n → ∞ a n does not exist, or if lim n → ∞ (a n ≠ 0), then the series ∑ n = 1 ∞ (a n) is divergent. This is an alternating series and is convergent. 1/5 + 1/25 + 1/125 + 1/625 a) it diverges;
Source: slideplayer.com
The limit of the sequence terms is, lim n → ∞ n ( n + 1) 2 = ∞ lim n → ∞ n ( n + 1) 2 = ∞. Which of the following are improper uses of the comparison test? Show the work that leads to your conclusion.
Source: chegg.com
The nth term for divergence states that if lim n → ∞ a n does not exist, or if lim n → ∞ (a n ≠ 0), then the series ∑ n = 1 ∞ (a n) is divergent. The absolute value is bounded above by 1/n!, which has a ratio which converges to 0 (in fact, its sum is e). Show the work that leads to your conclusion.
Also Read :
