That only one of two factors can be squared to give you the trinomial. An expression acquired from the square of the binomial equation is a perfect square trinomial.
Which Of The Following Is A Perfect Square Trinomial. Δ = b 2 − 4 a c = − 1 2 2 − 4 ( 4) ( 9) = 0. Otherwise the given trinomial is not a perfect square. 16 is a perfect square of 4 times 4, and 9 is a perfect square of 3 times 3. Therefore, a perfect square trinomial can be defined as an expression that is obtained by squaring a binomial
📈Which Of The Following Is A Perfect Square Trinomial? - Brainly.com From brainly.com
Related Post 📈Which Of The Following Is A Perfect Square Trinomial? - Brainly.com :
In the example here, 2*n = b = 24. (n + 5) (n + 2) b. (n + 1) (n + 6) c. If the first and last terms are perfect squares, and the middle term’s coefficient is twice the product of the square roots of the first and last terms, then the expression is a perfect square trinomial.
So n = 12, and c = n^2 = 144.
Which of the following or properties of a perfect square trinomial? Factor the following perfect square trinomial using the rule(b/2) 2: A perfect square trinomial is a trinomial that can be written as the square of a binomial. The components, a and b , that make up the perfect square trinomial can be constants. Moreover, which shows a perfect square trinomial? Otherwise the given trinomial is not a perfect square.
Source: youtube.com
Similarly, a binomial is an expression composed of two terms. If we are able to write the given trinomial in the above form, then it is perfect square. The excellent square formula takes the following kinds:
Source: chegg.com
Recall that when a binomial is squared, the result is the square of the first term added to twice the product of the two terms and the square of the last term. Which of the following factors gives a product of n 2 + 7n + 6? A perfect square trinomial is one that can be factored to (x + n)^2.
Source: ck12.org
Similarly, a binomial is an expression composed of two terms. A quadratic expression is an expression whose highest exponent in the v. 4 x 2 − 1 2 x + 9.
Source: youtube.com
So n = 12, and c = n^2 = 144. The components, a and b , that make up the perfect square trinomial can be constants. Recall that when a binomial is squared, the result is the square of the first term added to twice the product of the two terms and the square of the last term.
Source: chegg.com
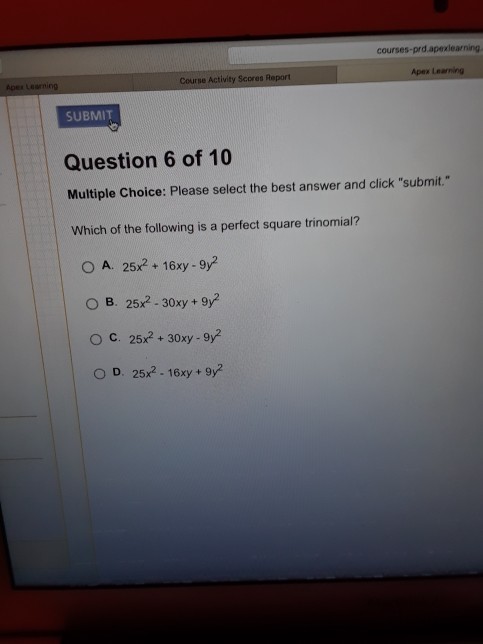
Which of the following or properties of a perfect square trinomial? You�ve solved a perfect square trinomial! Which of the following or properties of a perfect square trinomial?
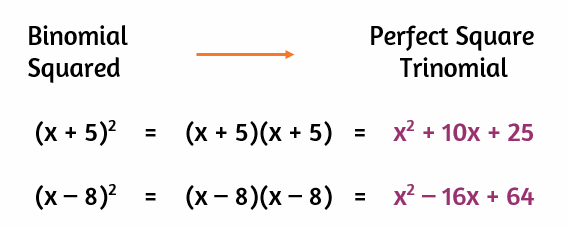Source: katesmathlessons.com
27/ [32 (2x+1)] just divided it. A trinomial is any equation of the form: You�re now ready to apply trinomial factoring to some practice problems.
Source: brainly.com
X2 16x + ____ 24 36 54 64. In the example here, 2*n = b = 24. So, we can write it as:
Source: topptutors.blogspot.com
A perfect square trinomial is a trinomial that can be written as the square of a binomial. A perfect square trinomial is a special type of trinomial. ( ax) 2 + 2abx + b2 = (ax + b) 2.
Source: youtube.com
Ax^2 + bx + c. When the binomial terms are multiplied by itself, then the resulting term is called a perfect square trinomial. In this case, a = 1, b = 24, and c is unknown.
Source: slideplayer.com
Similarly, a binomial is an expression composed of two terms. A quadratic expression is an expression whose highest exponent in the v. For example, if (a + 2) is a binomial, then the perfect square trinomial is obtained by multiplying (a+2) and (a+2), which gives a 2 + 4a + 4.
Source: cuemath.com
( ax) 2 + 2abx + b2 = (ax + b) 2. Otherwise the given trinomial is not a perfect square. X 2 + 6x + 4 b.
Source: quizizz.com
It means that, if f(a)= 0, f’(a) =0, but f”(a) is not zero, then the trinomial f(x) is said to be a perfect square. We must add the square of half of coefficient of x. X 2 + 6x + 4 b.
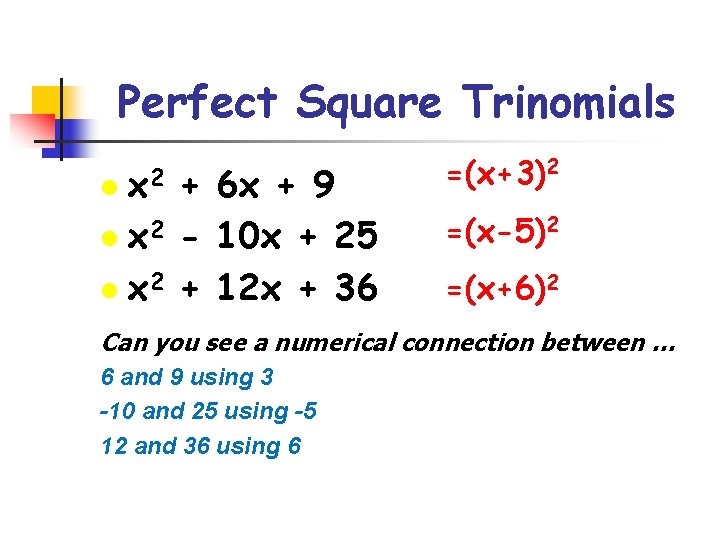Source: slidetodoc.com
[you can tell this is the case because if the trinomial is a perfect square, its factor must involve the square root of its first term and the square root of its last term. [you can tell this is the case because if the trinomial is a perfect square, its factor must involve the square root of its first term and the square root of its last term. Moreover, which shows a perfect square trinomial?
Source: basic-mathematics.com
To test whether the given trinomial is a perfect square, we should try to write the trinomial in the form of. All of the following are perfect square trinomials. If the first and last terms are perfect squares, and the middle term’s coefficient is twice the product of the square roots of the first and last terms, then the expression is a perfect square trinomial.
Source: study.com
A perfect square trinomial is formed by multiplying two binomials, which are one and the same. Recall that when a binomial is squared, the result is the square of the first term added to twice the product of the two terms and the square of the last term. Let’s take a look at the steps.
Source: slideplayer.com
An expression acquired from the square of the binomial equation is a perfect square trinomial. Moreover, which shows a perfect square trinomial? What square number must we add?
Source: andymath.com
4 x 2 − 1 2 x + 9. All of the following are perfect square trinomials. Play this game to review algebra i.
Source: onlinemathlearning.com
A quadratic expression is an expression whose highest exponent in the v. Similarly, a binomial is an expression composed of two terms. ( ax) 2 + 2abx + b2 = (ax + b) 2.
Source: brainly.com
What square number must we add? A quadratic expression is an expression whose highest exponent in the v. Let’s take a look at the steps.
Source: brainly.com
Otherwise the given trinomial is not a perfect square. How to factor a perfect square trinomial? Therefore, a perfect square trinomial can be defined as an expression that is obtained by squaring a binomial
Also Read :
