(b) find the local maximum and minimum values of f. So f of x is decreasing for x between d and e.
Find The Intervals On Which F Is Increasing And Decreasing. (c) find the intervals of concavity and the inflection points. This is the currently selected item. List the intervals on which the function is increasing and decreasing. $ f(x) = \frac{x}{x^2 + 1} $
Solved Find The Intervals On Which F(X) Is Increasing. The | Chegg.com From chegg.com
Related Post Solved Find The Intervals On Which F(X) Is Increasing. The | Chegg.com :
If f� (c) > 0 for all c in (a, b), then f (x) is said to be increasing in the interval. Cos 3𝒙putting f’(𝒙) = 0 3 cos. If f� (c) < 0 for all c in (a, b), then f (x) is said to be decreasing in the interval. Notice, these aren�t the same intervals.
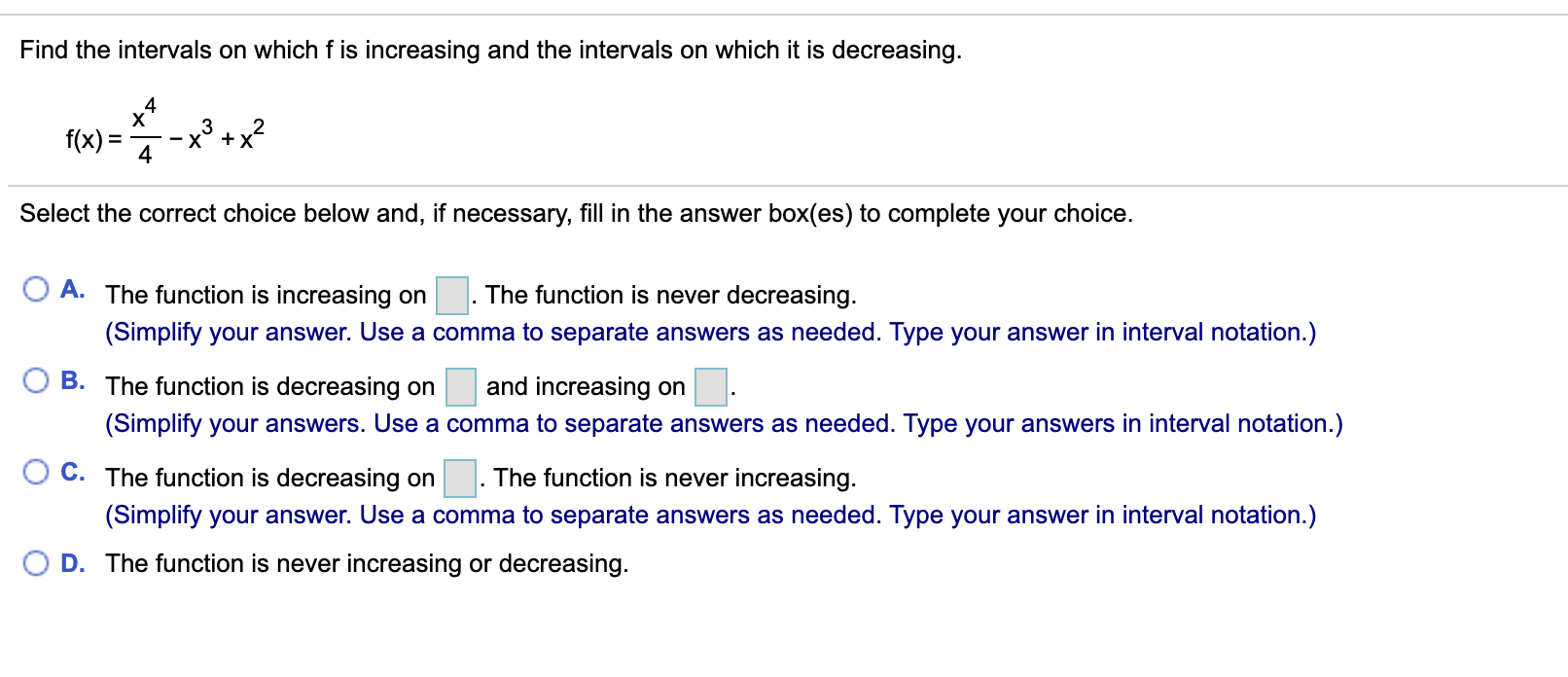
Find the intervals on which f is increasing and the intervals on which it is decreasing.
Determining intervals on which a function is increasing or decreasing. If f ′ ( x) < 0 on an open interval, then f is decreasing on the interval. If f(x) < 0, then the function is decreasing in that particular interval. For example, if you find the critical points to be x = − 2 and x = 7, then you must check the sign of f ′ ( x) for x ∈ ( − ∞, − 2), for x ∈ ( − 2, 7) and for x ∈ ( 7, ∞). (a) find the intervals on which $ f $ is increasing or decreasing. Find the intervals of increase and decrease of the, following functions.
![Use The Graph To Determine Open Intervals On Which The Function Is Increasing, Decreasing, Or Constant. [Solved]](https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/use-the-graph-to-determine-open-intervals-on-which-the-function-is-increasing-02-1622560519.png "Use The Graph To Determine Open Intervals On Which The Function Is Increasing, Decreasing, Or Constant. [Solved]")
Source: cuemath.com
(b) find the local maximum and minimum values of $ f $. The interval is increasing if the value of the function f (x) increases with an increase in the value of x and it is decreasing if f (x) decreases with a decrease in x. Finding decreasing interval given the function.
Source: study.com
(b) find the local maximum and minimum values of f. For example, if you find the critical points to be x = − 2 and x = 7, then you must check the sign of f ′ ( x) for x ∈ ( − ∞, − 2), for x ∈ ( − 2, 7) and for x ∈ ( 7, ∞). Evaluate the derivative at a point in each subinterval to determine.
Source: nagwa.com
F(𝑥) = sin 3𝑥 where 𝑥 ∈ [0 ,𝜋/2]finding f’(x)f’(𝑥) = 𝑑(sin3𝑥 )/𝑑𝑥 f’(𝑥) = cos 3𝑥 × 3 f’(𝒙) = 3. Find the intervals on which f is increasing and the intervals on which it is decreasing. So hopefully that gives you a sense of things.
Source: youtube.com
Finding decreasing interval given the function. So if we want to find the intervals where a function increases or decreases, we take its derivative an analyze it to find where it’s positive or negative (which is easier to do!). The derivative of a function may be used to determine whether the function is increasing or decreasing on any intervals in its domain.
Source: nagwa.com
If f� (c) > 0 for all c in (a, b), then f (x) is said to be increasing in the interval. Finding increasing interval given the derivative. So if we want to find the intervals where a function increases or decreases, we take its derivative an analyze it to find where it’s positive or negative (which is easier to do!).
Source: mathematica.stackexchange.com
To find increasing and decreasing intervals, we need to find where our first derivative is greater than or less than zero.to find intervals on which (f) is increasing and decreasing:to find the an increasing or decreasing interval, we need to find out if the first derivative is positive or negative on the given interval. Find the intervals of increase and decrease of the, following functions. Cos 3𝒙putting f’(𝒙) = 0 3 cos.
Source: chegg.com
If f(x) > 0, then the function is increasing in that particular interval. Recall that, if f � > 0 on a given interval, then f is increasing on that interval, and when f � < 0 on a given interval, then f is decreasing on that interval. If f(x) > 0, then the function is increasing in that particular interval.
Source: nagwa.com
If f(x) < 0, then the function is decreasing in that particular interval. The derivative of a function may be used to determine whether the function is increasing or decreasing on any intervals in its domain. Ponder the graphs in the box above until you are confident of why the two conditions listed are true.
Source: slideshare.net
Determining intervals on which a function is increasing or decreasing. Analytically, we find these intervals using the following process: That we are, the intervals where we�re positive or negative don�t perfectly coincide with when we are increasing or decreasing.
Source: chegg.com
(a) find the intervals on which f is increasing or decreasing. (b) find the local maximum and minimum values of $ f $. Analytically, we find these intervals using the following process:
Source: chegg.com
Find the intervals in which f (x)=s in\ x (1+cosx),\ \ 0<x<pi/2 is increasing or decreasing: F (x) = (2 x − 1) (2 x − 2) 2 For example, if you find the critical points to be x = − 2 and x = 7, then you must check the sign of f ′ ( x) for x ∈ ( − ∞, − 2), for x ∈ ( − 2, 7) and for x ∈ ( 7, ∞).
Source: courses.lumenlearning.com
(b) find the local maximum and minimum values of $ f $. If 𝑓 is differentiable on an open interval, then 𝑓 is increasing on intervals where 𝑓 ′ ( 𝑥) > 0 and decreasing on intervals where 𝑓 ′ ( 𝑥) 0.in the graph above, the graph increases over the part that is.know how to use the rst and second derivatives of a function to nd intervals on which the function is increasing, decreasing, concave up, and concave down. Evaluate the derivative at a point in each subinterval to determine.
Source: khanacademy.org
Find the intervals on which f is increasing and the intervals on which it is decreasing. Finding increasing interval given the derivative. If f(x) > 0, then the function is increasing in that particular interval.
Source: youtube.com
The derivative of a function may be used to determine whether the function is increasing or decreasing on any intervals in its domain. If f ′ ( x) > 0 on an open interval, then f is increasing on the interval. So if we want to find the intervals where a function increases or decreases, we take its derivative an analyze it to find where it’s positive or negative (which is easier to do!).
Source: khanacademy.org
One of the major applications of derivatives is determining the monotonicity of a given function in a specific interval. To find increasing and decreasing intervals, we need to find where our first derivative is greater than or less than zero.to find intervals on which (f) is increasing and decreasing:to find the an increasing or decreasing interval, we need to find out if the first derivative is positive or negative on the given interval. Finding decreasing interval given the function.
Source: youtube.com
Finding intervals of increasing and decreasing. Find the intervals on which f(x) = x 4 − 8x 2 is increasing and decreasing. If 𝑓 is differentiable on an open interval, then 𝑓 is increasing on intervals where 𝑓 ′ ( 𝑥) > 0 and decreasing on intervals where 𝑓 ′ ( 𝑥) 0.in the graph above, the graph increases over the part that is.know how to use the rst and second derivatives of a function to nd intervals on which the function is increasing, decreasing, concave up, and concave down.
Source: chegg.com
This is the currently selected item. If f� (c) = 0 for all c in (a, b), then f (x) is said to be constant in the interval. Evaluate the derivative at a point in each subinterval to determine.
Source: chegg.com
Find the intervals of increase and decrease of the, following functions. (a) find the intervals on which $ f $ is increasing or decreasing. One of the major applications of derivatives is determining the monotonicity of a given function in a specific interval.
Source: youtube.com
The intervals where a function is increasing (or decreasing) correspond to the intervals where its derivative is positive (or negative). Evaluate the derivative at a point in each subinterval to determine. The derivative of a function may be used to determine whether the function is increasing or decreasing on any intervals in its domain.
Source: nagwa.com
Ponder the graphs in the box above until you are confident of why the two conditions listed are true. (c) find the intervals of concavity and the inflection points. Reading the function from left to right we can see that the function goes up.
Also Read :
